Verified Computer Arithmetic
Overview
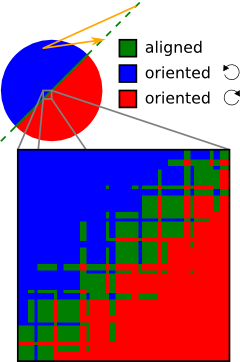
The floating-point arithmetic thematic aims at proving programs that contain computations on floating-point numbers, such as single or double precision numbers as defined by the IEEE-754 standard.
Floating-point arithmetic is primarily used as an efficient way of approximating arithmetic on real numbers. Due to its limited precision, floating-point computations may introduce inaccuracies in the numerical results. The picture on the right is an example of that. It shows the orientation of three points represented by the orange arrow. The extremal vertexes are fixed on the diagonal, while the middle point can move freely. The color (blue/green/red) at the position of the middle point shows the orientation. For instance, when this point is above the diagonal, the three points are oriented counter-clockwise, hence the color blue.
The orientation of the three points can be obtained by computing the determinant of a 2×2-matrix and looking at the sign of the result (5 subtractions, 2 multiplications). Zero means the three points are aligned; if positive, they are oriented one way; if negative, they are oriented the other way. While the computed sign seems correct overall, the lower part of the picture shows that the inaccuracies introduced by floating-point computations will produce an incorrect orientation for some positions of the middle point, in particular when the three points are almost aligned.
What Every Computer Scientist Should Know About Floating-Point Arithmetic
People
Former contributors: Tuyen Nguyen, Pierre Roux, Érik Martin-Dorel, Ali Ayad, Clément Fumex.
Research axes
Floating-Point Arithmetic
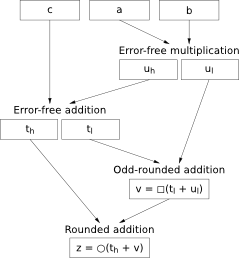
We are interested in verifying algorithms that perform floating-point computations to obtain intricate results. They are usually short but their purpose is not immediate from looking at their code. Indeed they are state-of-the-art devices that have been tuned beyond recognition by reordering operations, using function approximates, relying on exclusion principles, and so on, until a balance between accuracy and performance was reached. Testing is heavily used while developing such devices, but the extent of floating-point domains prevents the usage of exhaustive testing. That is why we are investigating methods and developing tools for formally verifying them and ensuring that all the behaviors have been accounted for.
We have developed Flocq, a generic formalization of floating-point arithmetic that is suitable both for verifying numerical programs and for computing inside a proof assistant. We have also formally proved the correctness of several algorithms that are often encountered as basic blocks: accurate polynomial discriminant, error-free transformations, emulation of fused-multiply-add operator (FMA), and so on. The picture on the right side presents the algorithm for emulating the FMA. Current case studies include floating-point expansions, numerical integration and numerical filters.
While we have been successful in manually writing formal proofs, it is an approach that does not scale well: verifying lengthy floating-point algorithms soon becomes tedious and time-consuming, even for experts in formal systems. So, we are also developing automated tools such as Gappa to verify arithmetic facts (domains, rounding errors, and so on) and to generate their formal proof.
Finally, formally verifying a floating-point algorithm would be pointless if the compiler was breaking it by inadvertently rearranging arithmetic operations during an optimization pass. So, we have also worked on formally verifying the way the CompCert C compiler handles floating-point numbers.
Integer Arithmetic and Interval Arithmetic
Floating-point arithmetic is not the only topic of computer arithmetic we are interested in. We are also working on arbitrary-precision integer arithmetic. Using the Why3 tool, we are developing a library that is compatible with the state-of-the-art GMP library, almost as fast, yet formally verified.
Multi-precision interval arithmetic is another of our research topics. We study it as a way to perform reliable computations in a formal setting, that is, Coq proofs. In particular, we have extended the CoqInterval library with some verified numerical integration algorithms based on robust polynomial approximations of elementary functions.
Numerical Analysis Programs
We aim at developing and applying methods to formally prove the soundness of programs from numerical analysis. It can be done in two steps: rounding error and method error. The rounding error corresponds to the accumulation of the round-off errors due to the floating-point computations of the values. We had to develop new complex methods as the usual techniques gave too large an error bound. The method error corresponds to the errors due to the discretization of the partial differential equation on a grid. The mathematical proofs from the literature have shown to be insufficient and we had to fill some holes in order to finish this formal proof.
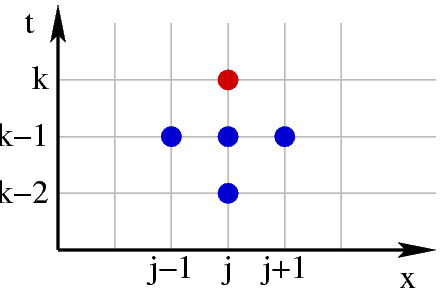
We have worked on the 1D acoustic wave equation, meaning the oscillation of a rope attached by its two ends as shown in the left picture. This partial differential equation is approximated by a second order centered finite difference scheme, also known as the “three-point scheme.” More precisely and as explained in the right picture, the value at pjk (red dot) depends on pj-1k-1, pjk-1, pj+1k-1, and pjk-2 (blue dots).
We are now interested in the finite element methods. For that, we have already proved the Lax-Milgram theorem. Now, the next mathematical properties we are interested in rely on the measure theory and Lebesgue integral we are currently formalizing in Coq.
Grants
Former grants:
- Standardization of interval arithmetic IEEE-1788 (Inria D2T)
- Digicosme working group ELFIC
- ANR-INS project VERASCO
- ANR project FOST
- RTRA Digiteo project Hisseo
Software and proofs
- Flocq (Floats for Coq) is a formalization of floating-point arithmetic for the Coq system. It provides a comprehensive library of theorems on a multi-radix multi-precision arithmetic; it also supports efficient numerical computations inside Coq.
- Gappa is a tool for automatically verifying properties on numerical programs dealing with floating-point or fixed-point arithmetic. While it is intended to be used directly, it can also act as a backend prover for the Why platform or as an automatic tactic for the Coq proof assistant.
- CoqInterval provides a Coq tactic for automatically proving some inequalities between real-valued expressions containing elementary functions.
- PFF is a Coq formalization of floating-point arithmetic with high-level definitions and high-level properties. It is now subsumed by the Flocq library.
See our gallery of verified programs or S. Boldo's gallery.
Main publications
- Jean-Michel Muller, Nicolas Brunie, Florent De Dinechin, Claude-Pierre Jeannerod, Mioara Joldes, Vincent Lefèvre, Guillaume Melquiond, Nathalie Revol, Serge Torres. Handbook of Floating-point Arithmetic (2nd edition). Birkhäuser Basel, 2018. [DOI]
- Sylvie Boldo and Guillaume Melquiond. Computer Arithmetic and Formal Proofs: Verifying Floating-point Algorithms with the Coq System. ISTE Press - Elsevier, December 2017.
- Assia Mahboubi, Guillaume Melquiond, Thomas Sibut-Pinote. Formally verified approximations of definite integrals. Journal of Automated Reasoning, March 2018. [DOI | full text on HAL]
- Sylvie Boldo, Stef Graillat, and Jean-Michel Muller. On the robustness of the 2Sum and Fast2Sum algorithms. ACM Transactions on Mathematical Software, 44(1), July 2017. [full text on HAL]
- Sylvie Boldo, Jacques-Henri Jourdan, Xavier Leroy, and Guillaume Melquiond. Verified compilation of floating-point computations. Journal of Automated Reasoning, 54(2):135--163, February 2015. [DOI | full text on HAL]
- Claude Marché. Verification of the functional behavior of a floating-point program: an industrial case study. Science of Computer Programming, 96(3):279--296, March 2014. [DOI | full text on HAL]
- Sylvie Boldo, François Clément, Jean-Christophe Filliâtre, Micaela Mayero, Guillaume Melquiond, and Pierre Weis. Wave equation numerical resolution: a comprehensive mechanized proof of a C program. Journal of Automated Reasoning, 50(4):423--456, April 2013. [DOI | full text on HAL]
PhD and habilitation
- Sylvie Boldo. Deductive Formal Verification: How To Make Your Floating-Point Programs Behave. Habilitation, Université Paris-Sud, October 2014.
- Thi Minh Tuyen Nguyen. Taking architecture and compiler into account in formal proofs of numerical programs. Thèse de doctorat, Université Paris-Sud, June 2012. [ full text on HAL | .pdf]