Invariant Generation in Kind2 and JKind
Personnes présentes
- Safouan Taha
- Frederic Boulanger
- Marie-Claude Gaudel
- Hai Nguyen Van
- Thibault Balabonski
- Delphine Longuet
- Vassil Todorov
- Burkhart Wolff
Presentators (by order of appearance)
- Bu
- Vassil Todorov
Background: Relevance of Invariant Generation for Random Testing
Presenter : bu
Random-Testing
Random-Testing is motivated by the observation that the number of paths grows usually exponentially with their length if drawn from practical transition systems or control flow graphs (CFG's).
There are known efficient algorithms that can draw from the path set in a statistically uniform manner long paths; and Marie-Claude investigated for quite some time the potential to use these algorithms for a test-generation method.
However, this approach meets a particular technical challenge: the probability that a drawn long path is feasible is also decreasing inverse exponentially with the length of the path in many practical examples.
Romain Aissat's Thesis on Infeasible Path detection
The thesis of Romain Aissat Infeasible Path Detection : a Formal Model and an Algorithm tries to overcome this "verrou technique" for the random-testing method by a transformation of the CFG into an equivalent one with less infeasible paths before drawing; his thesis shows an algorithm and a correctness proof see ITP paper. The algorithm consists of 6 graph transformation rules on so-called red-black graphs, which turn the originally black graph into a finally read one containing (usually) substantially less paths of a certain length that are infeasible. slides of an MTV2 Presentation 2016
Subsumption and Invariant Generation
A key problem is the subsumption rule of the graph transformation calculus which essentially establishes a simple invariant (simple in the sense: strong enough to establish reachability of the program end point, but usually too weak to establish the post-condition; the latter is just tested). The Algorithm of Romain used a number of heuristics that established a proof of concept, but not really a technology that scales reasonably well.
Invariant Generation in Recent Tools for Lustre
Recently, two SMT-based tools for the Lustre-Language (Kind2 and JKind) have been shown practically interesting which are based on invariant generators for k-induction schemes. Although the target language is different, the problem solved here is sufficiently similar to be relevant to random-based test generation.
Discussion of the Semantics of Lustre
Lustre follows the paradigm of a synchronous language where little blocks represent computation units that transform a stream of inputs to a stream of outputs while possessing a limited history on internal state variables.
Example:

There are various ways to consider the semantics of Lustre Programs such as:
- a Lustre program is an automaton
- a Lustre program is a stream processing function (as in Isabelle/HLL)
- a Lustre program is a co-algebra
- ... or just a notation for a While Loop and a non-terminating program
A pre-requisite of the latter view is a translation function that converts the equation systems in Lustre-nodes into an equation system over cells in the input and state streams.

As a result, the node above is compiled to:
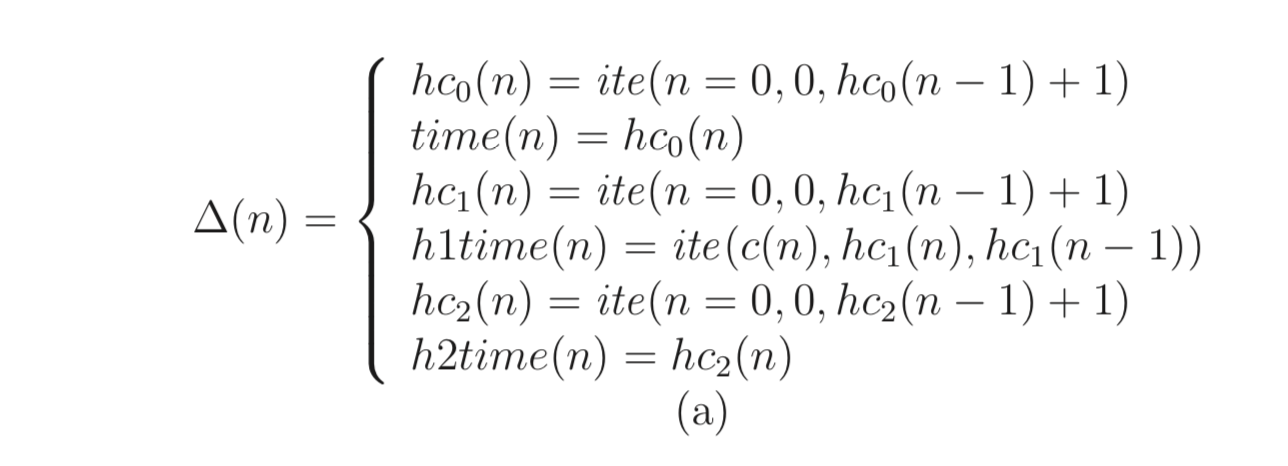
Note: this presentation is actually erroneous (but straight-forward), a corrected (but more involved) translation for ∆(n) is shown in Hagen's thesis on page 68.
The Lustre as a While-Loop-Idea was captured in the thesis of George Edward Hagen Verifying Safety Properties of LUSTRE Programs: An SMT-based appr. It has a number of advantages: More modern, more powerful deduction techniques (SMT instead of SAT), clean treatment of partial functions (division by zero, overflow in machine-arithmetics, ...) and seamless integration of C-calls verified by other tools.
The Lustre as a While-Loop Proof Method of a safety-property P is captured by the following pseudo-code:
(* initialize base *)
assert(∆(0)∧...∧∆(k));
assert(∆(0)∧...∧∆(k) ⟹ P(0)∧...∧P(k));
(* initialize step *)
n := 0;
while true do
begin
(* INV: ∆(n+1)∧...∧∆(n+k+1) ⟹ P(n+k+1) *)
∆(n) ; (* executing the body *)
n := n + 1;
end
Pragmatically, it is clear that this view of Lustre depends on strong mechanisms for invariant generation (which is obscured by the fact that Lustre flattens nodes and abandons internal structure).
These invariant generation heuristics are closely related to the ones needed for Aissat's subsumption rule (the k corresponds to the number of loop-unfoldings considered "above" a subsumption redex.)
The Architecture of JKind
Presenter : Vassil (and Safouan)
JKind is an inductive SMT-based model checker with invariant generation implemented in Java:
- Models and properties are specified in Lustre using the theories of
linear real and integer arithmetic
- It provides traceability between the proved property and individual model elements
- It supports simplifying and generalizing counterexamples to highlight to root cause of the failure
- Developed by Rockwell Collins and the University of Minnesota
JKind uses multiple parallel engines that are collaborating to prove or falsify properties:

- BMC (Bounded Model Checking): finds counterexamples for the base case of the k-induction
- k-ind: performs the inductive step of the k-induction
- InvGen (Invariant Generation): uses a template-based invariant generation technique having its own k-induction loop
- PDR (Property Directed Reachability): very advanced technique with backward model-checking together with invariant generation
- Advice: saves and uses invariants results between runs
JKind also implements:
- IVC (Inductive Validity Cores): is a subset of Lustre equations from the input model for which the property still holds => indicates which part of the model is relevant to the proof of the property
- Smoothing: uses a MaxSat query to smooth counterexamples minimizing the number of changes to the input variables
experiments
We used JKind to verify safety properties of a real Cruise Controller function. We chose Ansys Scade Suite R17.2 as modeling tool for its formally defined language based on Lustre. Thus the translation from Scade to Lustre was almost automatic. We can note that defining properties in Scade is easy because they are defined using the same library blocks as for the model. We formalized our properties from the safety-related requirements, extending them to all system high-level requirements (HLR) concerning the deactivation of the function. We want to prove that the cruise controller will be deactivated when any of the specified conditions occurs (e.g. a deceleration during 2s).
JKind verifies all the properties at the same time (incremental verification), so the proof of an easy property can help proving a difficult one. PDR/IC3 is essential and efficient for proving properties on big models, properties that consider a long period of time, and properties involving constants that are not exactly the same as in the code. We can summarize that JKind succeeds to prove all linear properties we formalized.