Personnes présentes

• Paolo Crisafulli
• Nicolas Meric
• Safouan Taha
• Burkhart Wolff

Presentators

• Burkhart Wolff

Summary:

Isabelle can be used to program logically safe extensions for specific formal methods support. And besides, Isabelle offers a cool programming environment for SML, and via reflection techniques also to OCaml, Haskell, and Scala.

This versatility of the Isabelle Platform has been applied for a number of projects such as HOL-TestGen, HOL-OCL, Isabelle/C, and Isabelle_DOF.

Bu recalled the Isabelle architecture, which is based on Kernel in the style of other members of the LCF-style provers such as HOL4, HOL-Light or Coq.

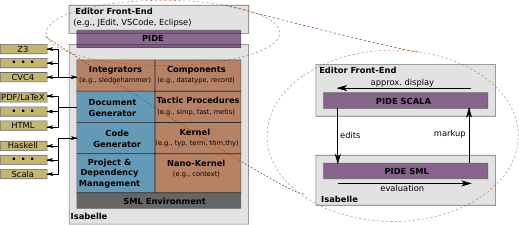
Abstract Isabelle Architecture

Over the SML environment, the kernel, the tactical proof layer, the specification construct support layer, the Isar-engine (the "Ìsar-toplevel") and the PIDE layer were built. Somewhat transversal are the code-generator and the document generator.

More details are given in a previous Isabelle/Club 20181106Meeting and in the technical report available here.

The Isabelle Kernel:

Bu shows how we can exchange with the SML layer from Isabelle/HOL using an ML<> cartouche

ML‹
  fun fac x = if x = 0 then 1 else x * (fac (x-1));
›

ML‹fac 5000›

ML‹open Int; open String; open List;›

So, it is possible to access the underlying SML programming environment, add and execute function definitions, and access the underlying modules (called "structures"), in this case some modules in the SML interpreter (the SML-"toplevel").

Now, the Isabelle Kernel Modules are *just* modules sitting in the SML toplevel. They can therefore accessed by:

ML‹open Term;›
ML‹open Thm;›
ML‹open Theory;›

The structure "Term" provides a conventional data-type for providing an abstract syntax for:

• types
• terms (with Curry-style type annotations)
• cterms (certified terms that must be well-typed)
• theories (containing, among many things, type and constant declarations)

There is a quite fantastic feature of the Isabelle/PIDE frontend: It is possible to annotate the underlying Isabelle implementation itself such that the *navigation* inside its own source becomes possible in the IDE. (Bu remembers only Smalltalk-like environments that were able to do this in the 80-ies...). The trick is done by the Isar command:

text‹@{file "ISABELLE_HOME/src/Pure/ROOT.ML"}›

Clicking on ML-representations in the PIDE output window allows for direct navigation and inspection in the SML-source of Isabelle!

We recall that we can access, e.g., theorems by inspection commands at the Isar-level:

thm refl 

Now, it is possible to use antiquotations at the ML level to access the Lambda-term structure of the theorem "refl".

ML‹
  val r = @{thm refl};
  concl_of r;
  cprop_of r;
›

The operations "concl_of" from the Term-module allows to directly *see* the internal lambda-representation of Isabelle.

Antiquotations for types and terms help to achieve this effect directly on the SML-level:

ML‹
  val m = @{term ‹(a::int) + x›};
  val n = @{typ ‹'a list›}; 
  val Type(a, S) = @{typ ‹'a list›}; 
  val Type(a, [TFree(x, y)]) = @{typ ‹'a list›};
›

Note that the SML-toplevel pretty-printer is configured to represent types compactly, and this is sometimes misleading. Via pattern-matching we can access the internal structure of the types step by step.

There are also useful antiquotations for the global and local contexts inside the (Isabelle-)SML command:

ML‹
  @{theory};
  @{context};
›

Now, in order to produce a term, convert it into a formula, and then insert it, e.g., as definition into some global context, one has to produce type-correct ("certified") lambda-terms. There are fundamentally two ways to do this:

• one puts in the terms always the joker dummyT whenever a type-expression is needed in the terms and lets the type-inference fill in the gaps. Easy, but at times problematic since the inferred type may be too general, and lead to definitions which are actually unusable in proofs.
• one uses a library to construct exact types; fastype_of may help if we construct bottom-up well-typed terms from well-typed terms. (if its argument is not exactly typed (no dummyT) and well-typed, this function may produce somewhat arbitrary results).

For HOL, a library of such *typing* term-constructors is already provided:

ML‹
  open HOLogic;
›

With the antiquotation @{const_name ...} one can make sure that the string argument is indeed the denotation of a constant symbol in the surrounding logical context:

ML‹
  @{const_name "HOL.True"};
  val X =  \<^const_name>‹HOL.True›;

  val TT = Const (@{const_name‹Pure.eq›}, dummyT --> dummyT --> propT);
›

Now, we can construct an equation in the Pure-logic by an own function that creates such lambda-terms and types them from (some) types in the leaves of its argument term (Which is ok for the case that this term is already correctly typed).

ML‹
  fun meta_eq_const T = Const (@{const_name‹Pure.eq›}, T --> T --> propT);
  fun mk_meta_eq (t,u) = meta_eq_const (fastype_of t) $ t $ u;

  val X = mk_meta_eq (HOLogic.Suc_zero, HOLogic.zero);
  cterm_of @{context} X;


  val X = mk_meta_eq (HOLogic.Suc_zero, HOLogic.imp);
  cterm_of @{context} X;

›

Thus, we can construct a type-correct and an ill-typed term and try to certify it in the context: in the first case, this will succeed, in the second case, this will fail.

Summing up: The internal lambda-term presentation is very close to text-book representation of the Curry-style typed lambda calculus. The SML environment and the use of antiquotations makes it possible to program all sorts of computations over them in a fairly elegant, development-stable and logically safe way.

We can use pattern matching to unify variables and to write ML code to extend the kernel!